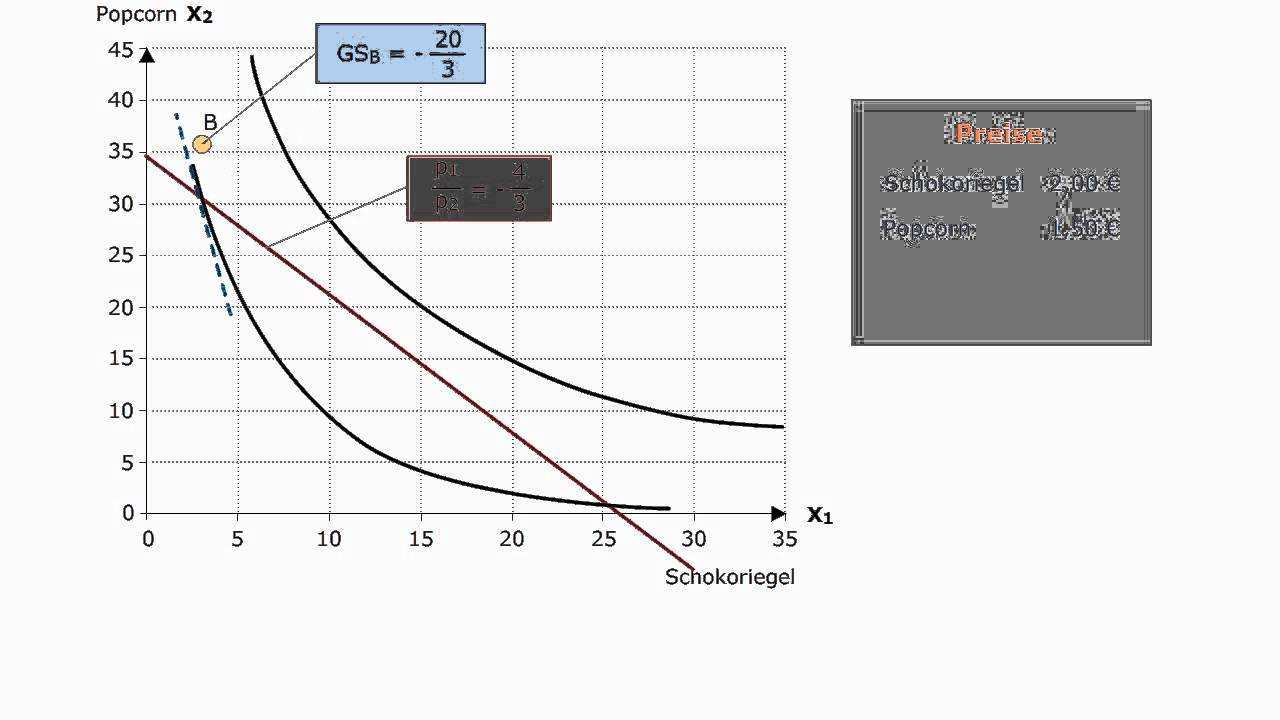
Haushaltsoptimum Berechnen Beispiel

Der haushalt erreicht den größtmöglichen nutzen wenn er sein einkommen für das güterbündel p ausgibt also 100 x und 125 y kauft wie man aus der grafik mit der methode des scharfen hinsehens ermitteln kann.

Haushaltsoptimum berechnen beispiel. Der preis einer einheit von gut 1 beträgt p. Nutzenmaximierung in der haushaltheorie. Aber wir wissen ja dass das nutzenniveau umso höher ist je weiter die indifferenzkurve vom ursprung entfernt ist. Du leitest mit der produkt und ggf.

1 x 1 2 x 2 60 x 1 hat einen. Du wählst einfach irgendein güterbündel auf der budgetgeraden beispielsweise burger und bier. Auf diesen beitrag antworten hi abakus danke für deine willkommensgrüße und deine lösungsfunktionen. Die nutzenfunktion war u x 1 x 2 2 x 1 x 2 mit x 1 für die menge von gut 1 und x 2 für die menge von gut 2.

Aufgabe 1 12 punkte horsts nutzenfunktion ist gegeben durch u x 1 x 2 x2 4x2 2. Die nutzenfunktion u x 1 x 2 sei 2 x 1 x 2 mit x 1 für die menge von gut 1 und x 2 für die menge von gut 2. Dann gilt d h die grenzrate der substitution indifferenzkurven ist gleich dem negativen reziproken verhältnis der güterpreise. Das haushaltsoptimum ist im tangentialpunkt p mit den mengen y und i von bilanzgerade und höchsterreichbarer indifferenzkurve gegeben wobei die bilanzgerade zur substitutionstangente wird.

Grenzrate der substitution preisverhältnis. Zur bestimmung des betriebsoptimums benötigen sie eine kostenfunktion die ihre betriebliche kostenstruktur möglichst genau abbildet. Die grenzrate der substitution ist 2 x 2 2 x 1 x 2 x 1. Der punkt p heißt haushaltsoptimum oder haushaltsgleichgewicht.

In einfachen beispielen betrachtet man häufig den ein produkt fall da dieser nicht so komplex ist das aufstellen der formel relativ einfach ist und die vorgehensweise trotzdem gut veranschaulicht wird. Dann ist der grenznutzen mu 1 ableitung der nutzenfunktion nach x 1 2 x 2 und der grenznutzen mu 2 ableitung der nutzenfunktion nach x 2 2 x 1.